#230 Inherited Resources

In this episode we’re going look at a gem by José Valim called Inherited Resources. This gem extracts common functionality from RESTful controllers and lets you remove duplication from controller code. This isn’t the first Rails gem that provides this type of help, episode 92 covered a gem called make_resourceful and there are other plugins available too. Each takes a slightly different approach and are worth taking a look at before you decide which one to use, if any. We’ve chosen Inherited Resources as it works well with Rails 3.0 and feels a little more up-to-date.

The Rails application we’ll be working with in this episode is a simple e-commerce application. This application has a list of products and each product has a number of associated reviews.

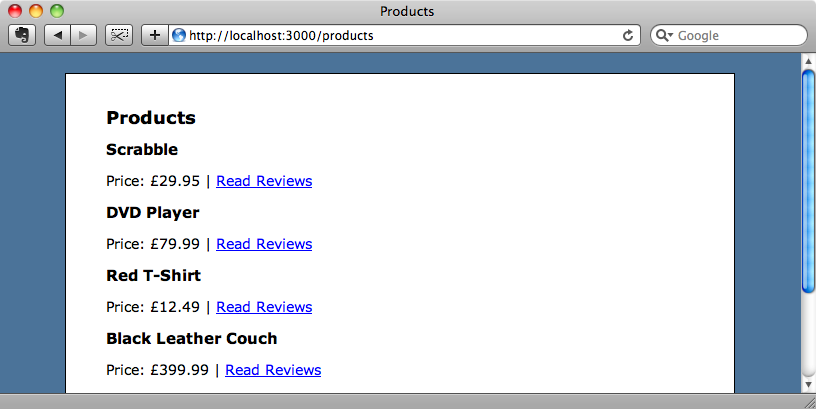
We’ll use Inherited Resources to clean up the internals of this application and see how much controller code we can remove without affecting the functionality.

Installing Inherited Resources

The ProductController’s code currently looks like this.

class ProductsController < ApplicationController
  def index
    @products = Product.all
  end

  def show
    @product = Product.find(params[:id])
  end

  def new
    @product = Product.new
  end
  
  def create
    @product = Product.new(params[:product])
    if @product.save
      flash[:notice] = "Successfully created product."
      redirect_to @product
    else
      render :action => 'new'
    end
  end
  
  def edit
    @product = Product.find(params[:id])
  end
  
  def update
    @product = Product.find(params[:id])
    if @product.update_attributes(params[:product])
      flash[:notice] = "Successfully updated product."
      redirect_to @product
    else
      render :action => 'edit'
    end
  end
  
  def destroy
    @product = Product.find(params[:id])
    @product.destroy
    flash[:notice] = "Successfully destroyed product."
    redirect_to products_url
  end

end

If you have a number of RESTful controllers in your application you’ll find yourself writing code like this in each one of them and it’s in situations like these that Inherited Resources is most useful. If, however, you generally customize your controllers quite heavily then an abstraction like Inherited Resources may not suit your needs. The controller code above follows the RESTful pattern quite closely so we can use it to see what Inherited Resources provides.

source 'http://rubygems.org'

gem 'rails', '3.0.0'

gem 'sqlite3-ruby', :require => 'sqlite3'
gem 'nifty-generators'
gem 'inherited_resources'

It’s then installed in the usual way with

$ bundle install

This will install the gem along with a couple of dependencies: has_scope and responders.

Once the gems are installed we can update our ProductsController to use Inherited Resources. To do this we make the controller inherit from InheritedResources::Base instead of ApplicationController. InheritedResources::Base inherits from ApplicationController so it will have all of its functionality.

As the ProductsController is a pretty standard RESTful controller we can replace all of its methods with the code inherited from Inherited Resources, leaving the controller code quite a bit shorter.

class ProductsController < InheritedResources::Base

end

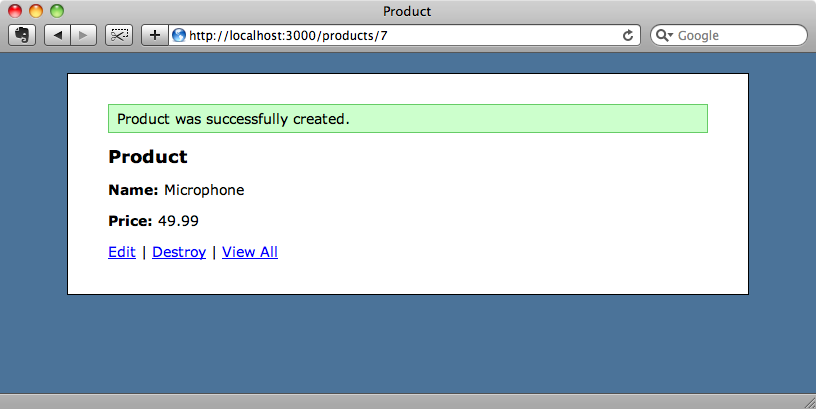
We’ll need to restart the server to get the new gems loaded but once we do we’ll see that the pages related to products work just as they did before. We can even create a new product successfully and the appropriate flash message is shown when we do so.

Customizing an Action

When we created a new product above we were redirected to that product’s show page afterwards, but what if we want the application to redirect to the index action instead? Inherited Resources allows us to override any of its default actions by simply overriding the relevant method in the controller so we could write a create method in the ProductsController that would create the new product and then redirect to the index action.

There’s no need, though, to completely rewrite the create action just to change the redirect. We can include Inherited Resource’s behaviour by calling create! and passing it a block. Changing the redirect URL when a new model object is created successfully is a common thing to want to do and so we can simply return the desired URL in a block.

class ProductsController < InheritedResources::Base
  def create
    create! { products_path }
  end
end

There are other things we can do in the block and these are explained in the documentation.

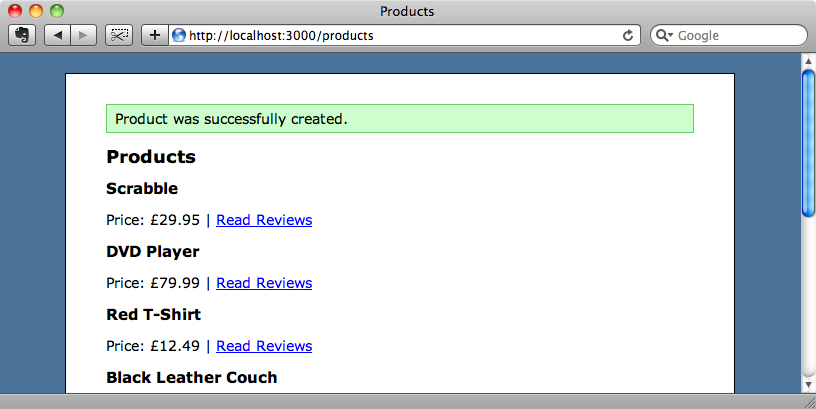
Now when we create a new product we’re redirected to the index action just like we want.

Working With Different Formats

If we want our controller to be able to respond to different formats, say to work with XML as well as HTML, it’s easy to do this. All we need to do is add respond_to as we would with any other Rails 3 controller.

class ProductsController < InheritedResources::Base
  respond_to :html, :xml

  def create
    create! { products_path }
  end
end

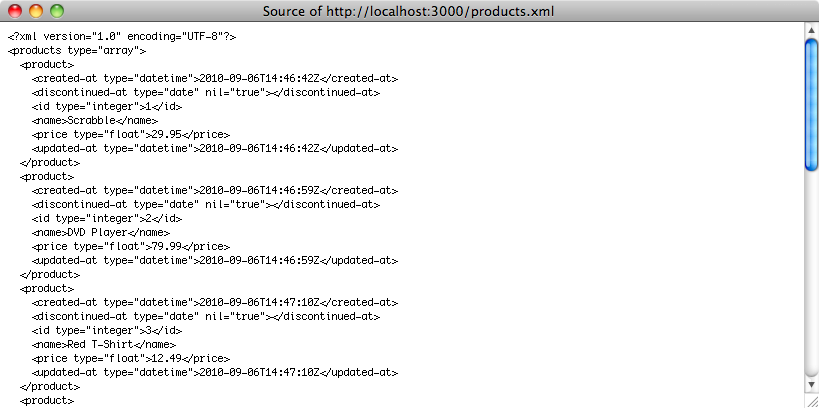
This will work in the same way we showed in episode 224 [watch4, read5]. If we visit /products.xml now we’ll get a list of products in XML.

Nested Resources

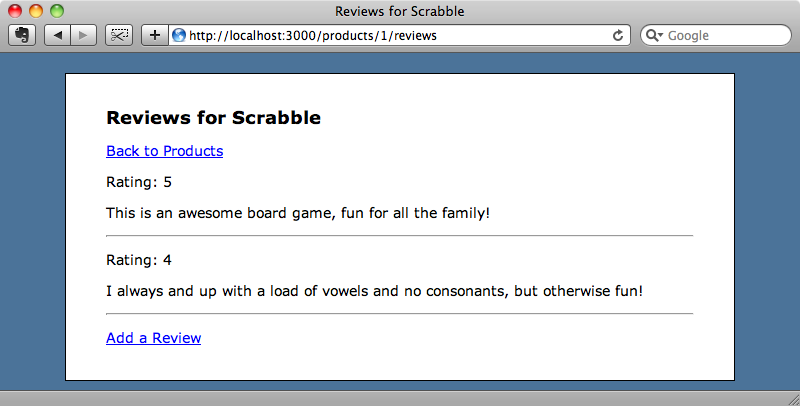
Now that we’ve tidied up the ProductsController, lets move on to the ReviewsController. Reviews are nested under products so if the reviews for an article we’ll be at the URL /products/1/reviews for the product with an id of 1. This is the index action of the ReviewsController. Likewise if we add a review the URL will still be nested under products.

The code for the ReviewsController looks like this:

class ReviewsController < ApplicationController
  def index
    @product = Product.find(params[:product_id])
    @reviews = @product.reviews
  end

  def new
    @product = Product.find(params[:product_id])
    @review = Review.new
  end
  
  def create
    @product = Product.find(params[:product_id])
    @review = @product.reviews.build(params[:review])
    if @review.save
      flash[:notice] = "Successfully created review."
      redirect_to product_reviews_path(@product)
    else
      render :action => 'new'
    end
  end

end

The immediate difference between this controller and the ProductsController is that it only has three of the seven RESTful actions. The other difference is that, because it handles nesting, each action gets a product based on a parameter in the URL.

Even though we have a nested resource here the behaviour is fundamentally the same as in the ProductsController and Inherited Resources will still work well here. We can remove the existing code in the controller and change the class so that it inherits from InheritedResources::Base. All we need to do to handle the nesting is use belongs_to, which is a method that Inherited Resources provides and which can be used in define relations between controllers in the same way that they’re defined between models. With this in place Inherited Resources handles fetching the correct product for us.

class ReviewsController < InheritedResources::Base
  belongs_to :product
end

As it stands the ReviewsController will have all seven actions, as this is Inherited Resources’ default behaviour, but we want this controller to only respond to index, new and create. We can use the actions method to restrict the actions that are available.

class ReviewsController < InheritedResources::Base
  belongs_to :product
  actions :index, :new, :create
end

As we did with the ProductsController we want to change the URL that we redirect to after creating a new review. There are a number of URL helper methods that Inherited Resources provides to redirect to various actions, which is useful here as we have some nesting here. In this case we can use a method called collection_url which will redirect to the index action and handle the nesting for us.

class ReviewsController < InheritedResources::Base
  belongs_to :product
  actions :index, :new, :create
  
  def create
    create! { collection_url }
  end
end

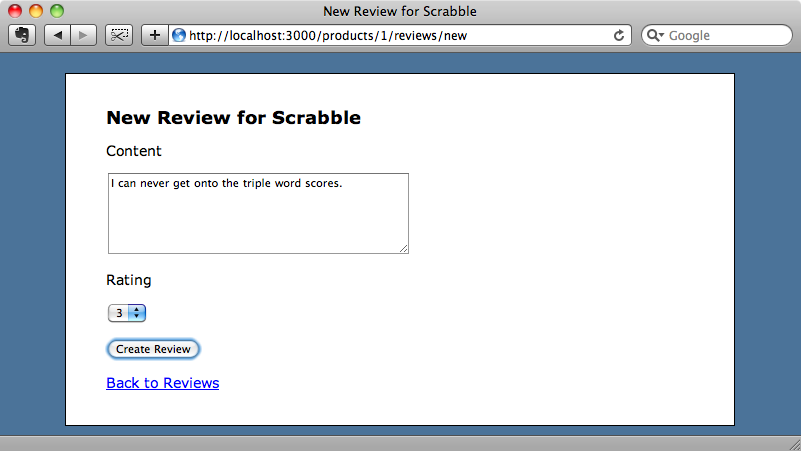
We can test this by adding a review.

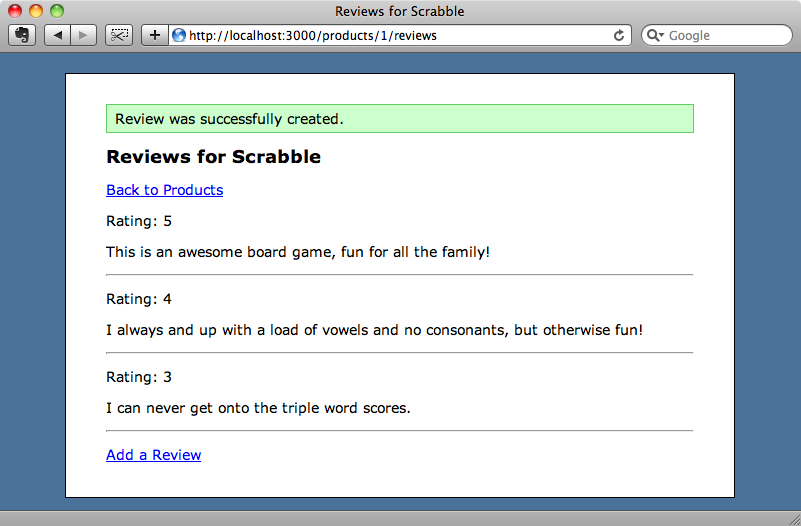
After we submit the new review we’ll be redirected to the reviews page for that product just as we want.

Public Scopes

Inherited Resources has another useful feature called has_scope. To use it we just need to add a reference to the gem in the Gemfile and then run bundle install again.

source 'http://rubygems.org'

gem 'rails', '3.0.0'

gem 'sqlite3-ruby', :require => 'sqlite3'
gem 'nifty-generators'
gem 'inherited_resources'
gem 'has_scope'

With this installed we can call has_scope in any of our controllers and pass it the name of a scope on the related model. For this example we’ll add the limit scope, which is provided by default to all Rails 3 models, to the ProductsController.

class ProductsController < InheritedResources::Base
  respond_to :html, :xml
  
  has_scope :limit

  def create
    create! { products_path }
  end
end

With this in place we can add scopes as parameters to the URL, so if we pass in a limit parameter that scope will be called and we’ll restrict the number of products that are shown.

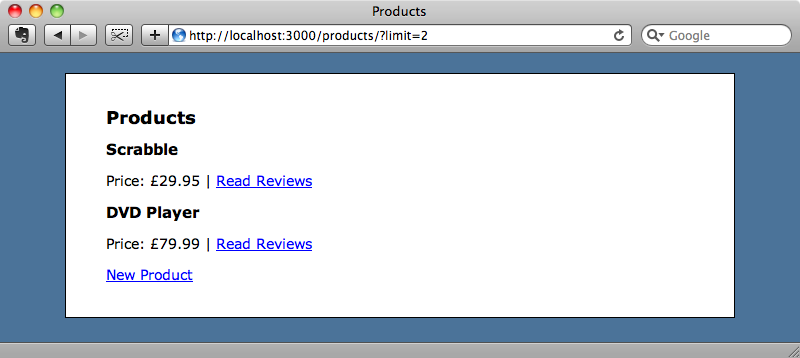
If we want the scope to be applied all the time even when it’s not mentioned in the query string, we can pass in a default value.

class ProductsController < InheritedResources::Base
  respond_to :html, :xml
  
  has_scope :limit, :default => 3

  def create
    create! { products_path }
  end
end

Now, if we don’t pass in a limit parameter the default value will be used as we’ll see three products.

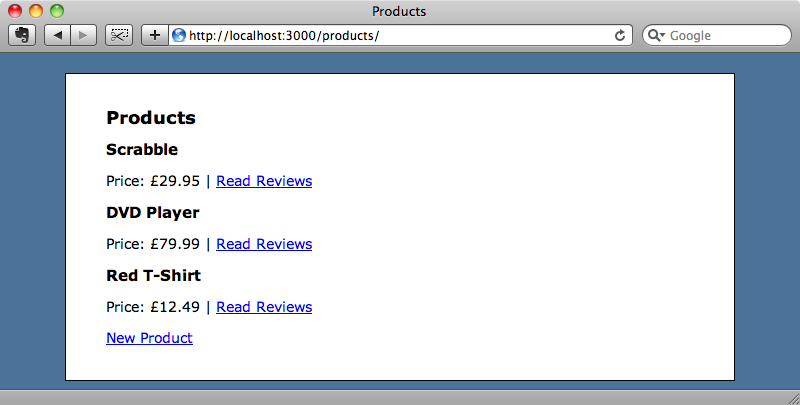
This works with custom scopes as well. We’ll add a scope to the Review model that will allow us to filter reviews by their rating.

class Review < ActiveRecord::Base
  belongs_to :product
  scope :rating, proc { |rating| where(:rating => rating) }
end

Now we’ll make the scope public by adding it to the ReviewsController.

class ReviewsController < InheritedResources::Base
  belongs_to :product
  actions :index, :new, :create
  has_scope :rating
  
  def create
    create! { collection_url }
  end
end

We can now use a rating parameter in the URL to restrict the reviews by their rating.

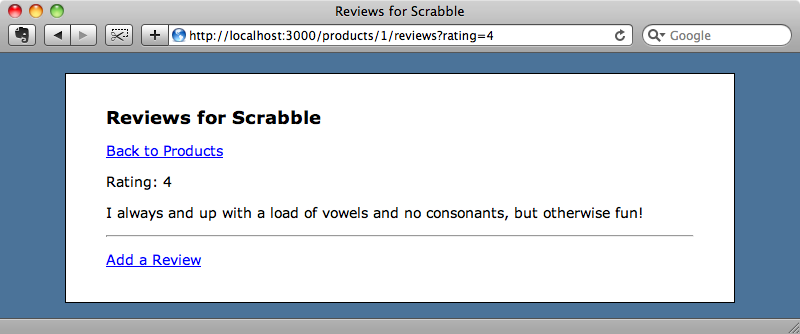
The has_scope gem can be used outside Inherited Resources by using the apply_scopes method inside the index action. There are more details about this in the documentation on Github.

Customizing The Flash Message

The last thing we’ll cover is how to customize the flash message. When we create a new review the default message is “Review was successfully created.” but we can alter this to be whatever we want by changing the internationalization files. Even if your application doesn’t support multiple languages these files are a great place to store strings that will be displayed in the user interface. Every Rails 3 application has an English localization file included in it at /config/locales/en.yml.

To override Inherited Resources’ default flash messages we create a flash: key, under which we have a key containing the name of the controller, in this case reviews:. Under there we add a key for the action and below that one for the name of the flash message. For our reviews controller the configuration file will look like this:

# Sample localization file for English. Add more files in this directory for other locales.
# See http://github.com/svenfuchs/rails-i18n/tree/master/rails%2Flocale for starting points.

en:
  flash:
    reviews:
      create:
        notice: "Your review has been created!"

If we don’t want to have to configure this for each controller in our application we can replace the controller name with actions: and then the messages will be applied to every single controller. We can use a resource_name variable placeholder to specify the name of the current model.

# Sample localization file for English. Add more files in this directory for other locales.
# See http://github.com/svenfuchs/rails-i18n/tree/master/rails%2Flocale for starting points.

en:
  flash:
    actions:
      create:
        notice: "Your {{resource_name}} has been created!"

We can test this out by creating a new review. When we submit it the custom flash message will be shown.

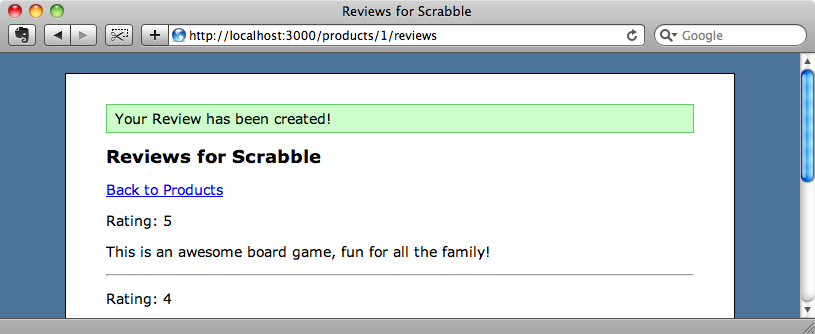
That’s it for this episode. If you find yourself creating the same controller code again and again then it’s well worth taking a look at Inherited Resources. The README file is fairly extensive and covers parts that we haven’t mentioned here. Likewise the wiki page is worth reading too.